Table of Contents
If you’re here then you’re probably done with Motion, if not, I suggest you go back and re-read it since there are going to be a lot of Motion elements in this blog.
But in case you forgot, let’s go over a few of the important ones:
- Displacement is a vector quantity which is defined as the change of position of an object. (m)
- Velocity is a vector quantity which represents the change in displacement over time. (m s-1)
- Acceleration is a vector quantity that represents the change is velocity over time. (m s-2)
1. Oscillations
Before stepping into Waves immediately, we first need to know a new type of motion which is common in all waves: OSCILLATIONS.
The word ‘Oscillation’ comes from the Latin word “To Swing”. It means to swing back and forth in a repeating motion. The time it takes for the an object to completely go back and forth or complete one oscillation is called the ‘Period‘. Examples of oscillation that you will see often in the IB exams are pendulums and springs. Here’s a clear GIF of a pendulum oscillating with no air resistance and friction.
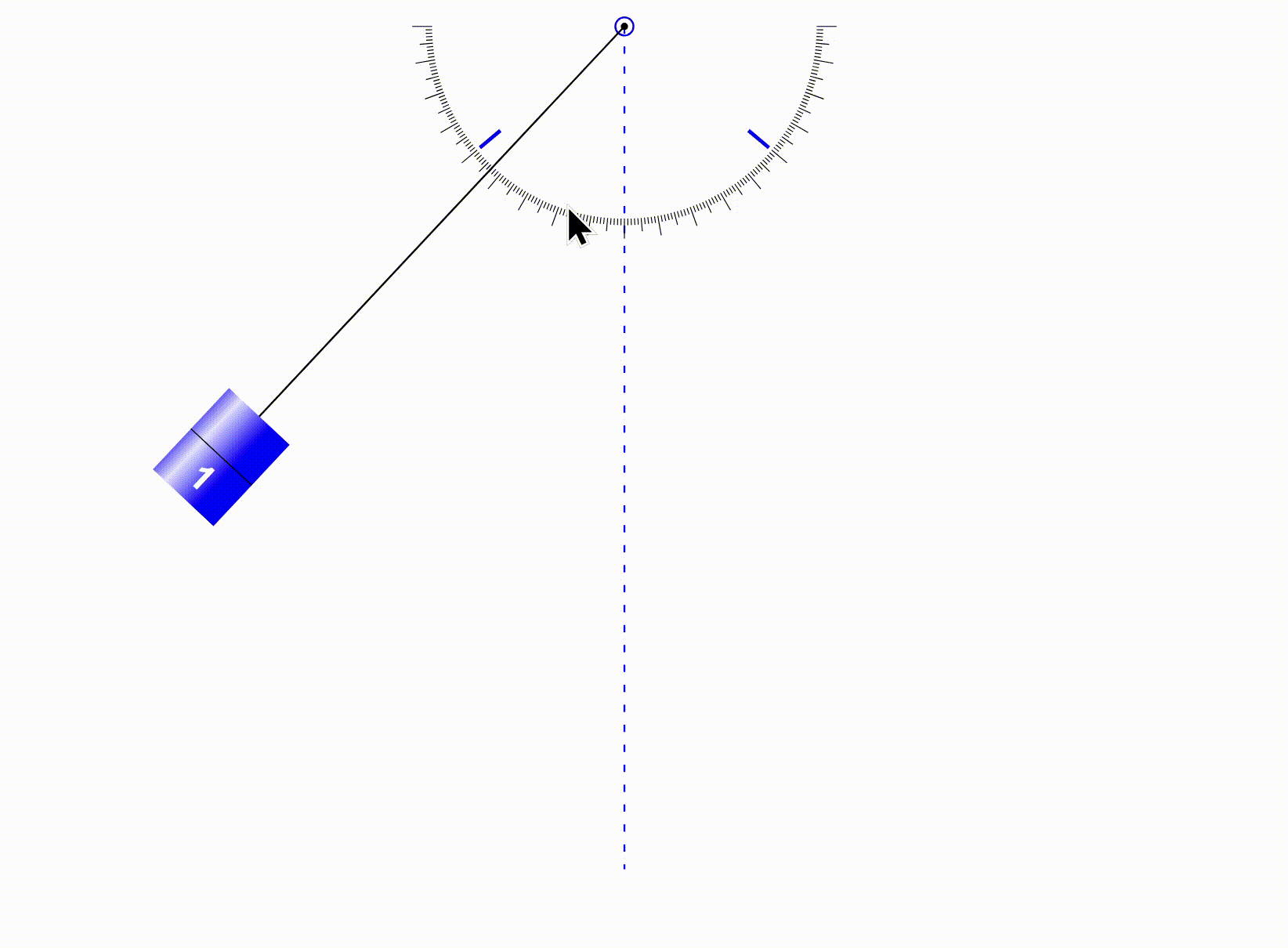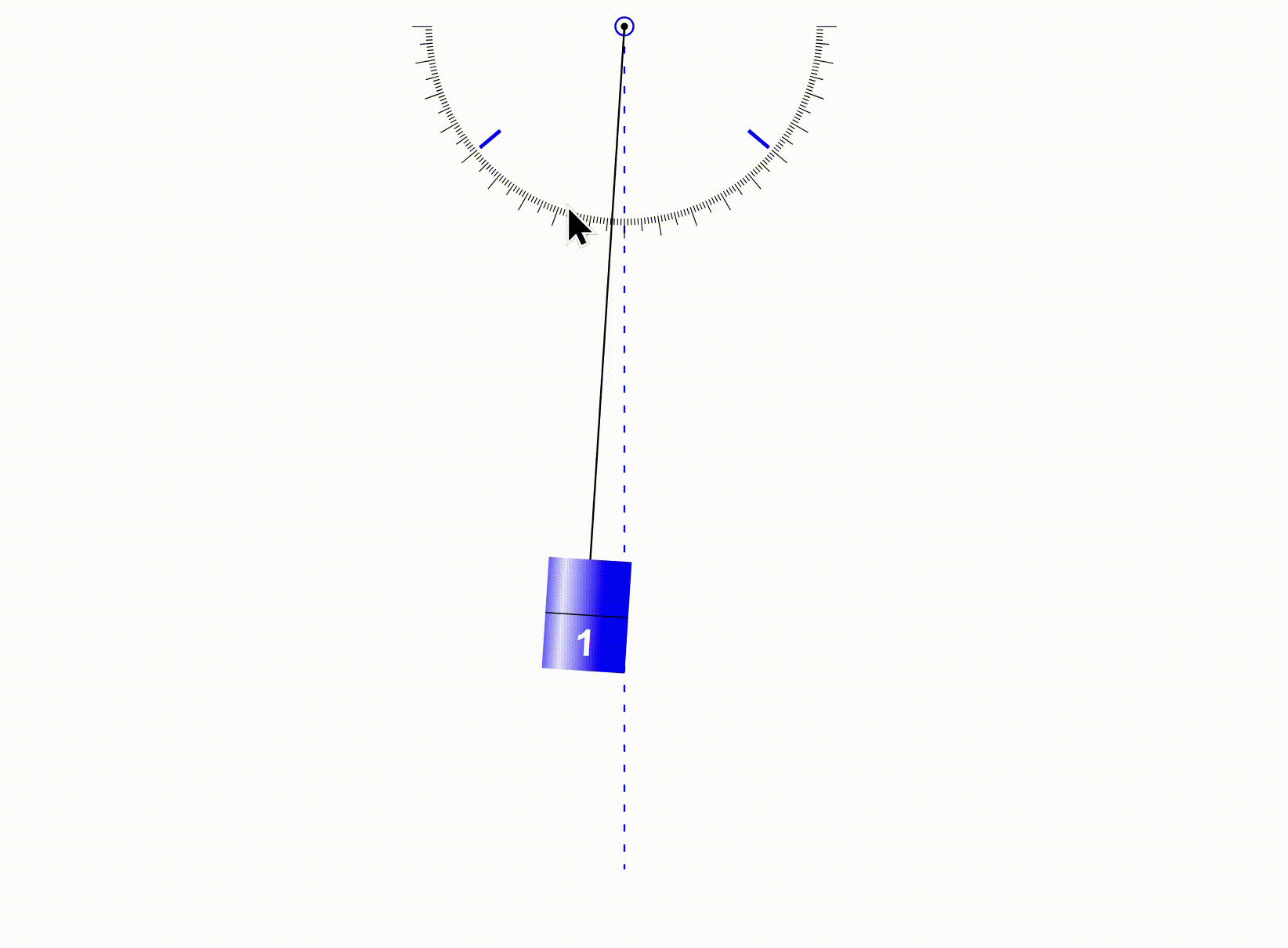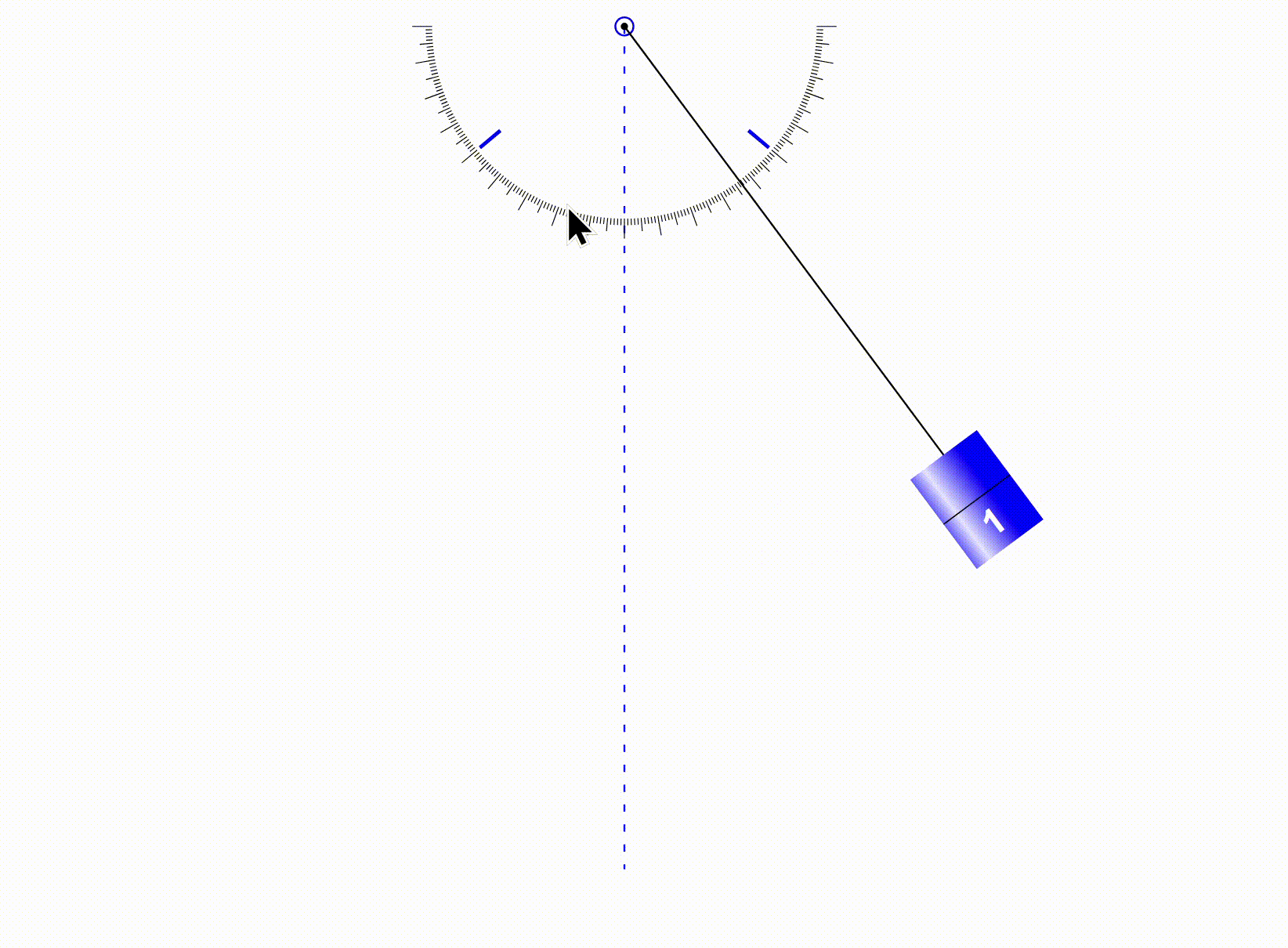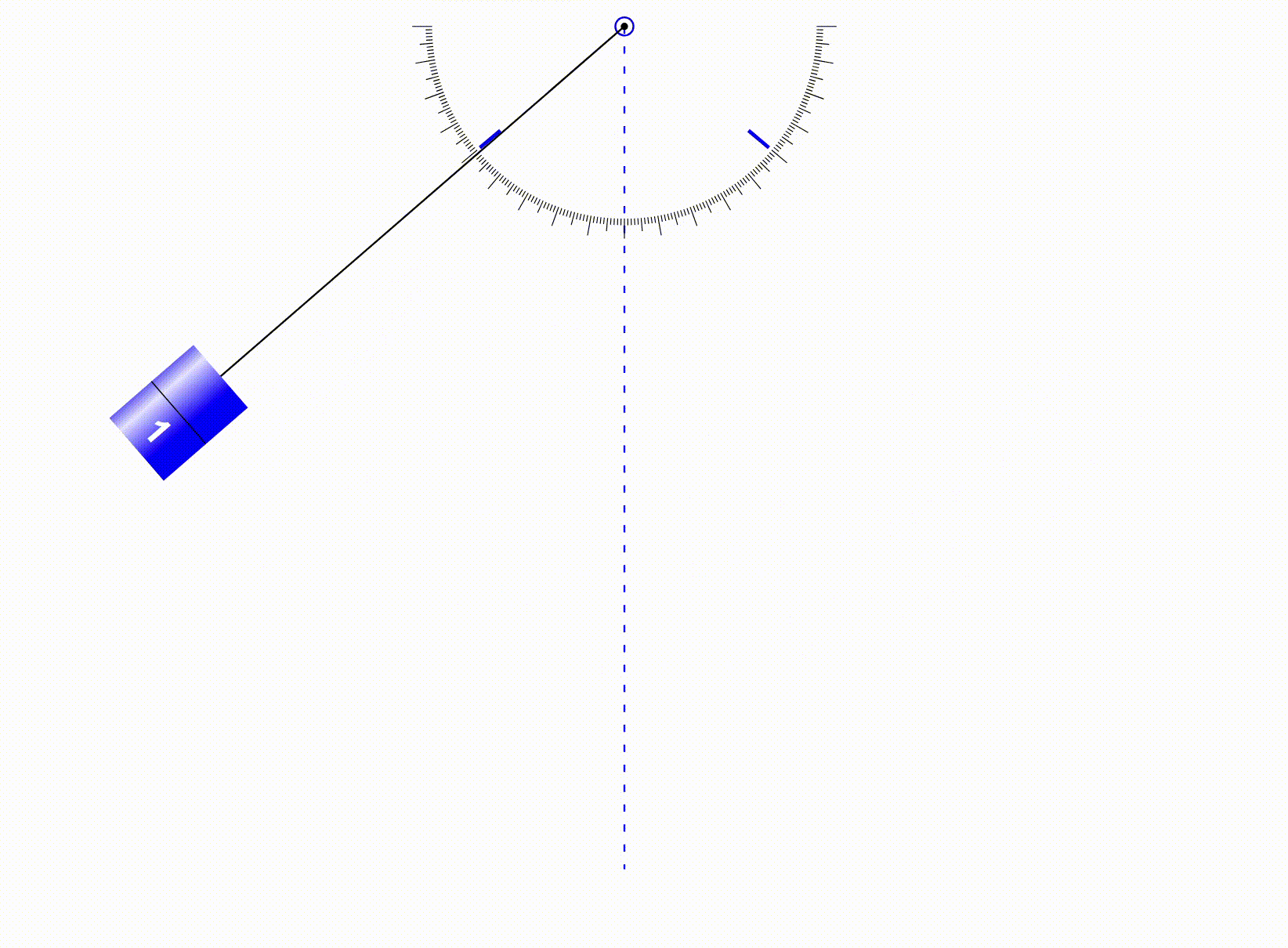
When the pendulum has reached its highest point on the left and right, velocity becomes 0. On the other hand, at this time, DISPLACEMENT is MAXIMUM. Displacement is only 0, when the pendulum is hanging straight down. Now, let us picture the motion above in the form of time graphs(NOTE: These graphs will not always have the same amplitude since that depends on each of the values provided):
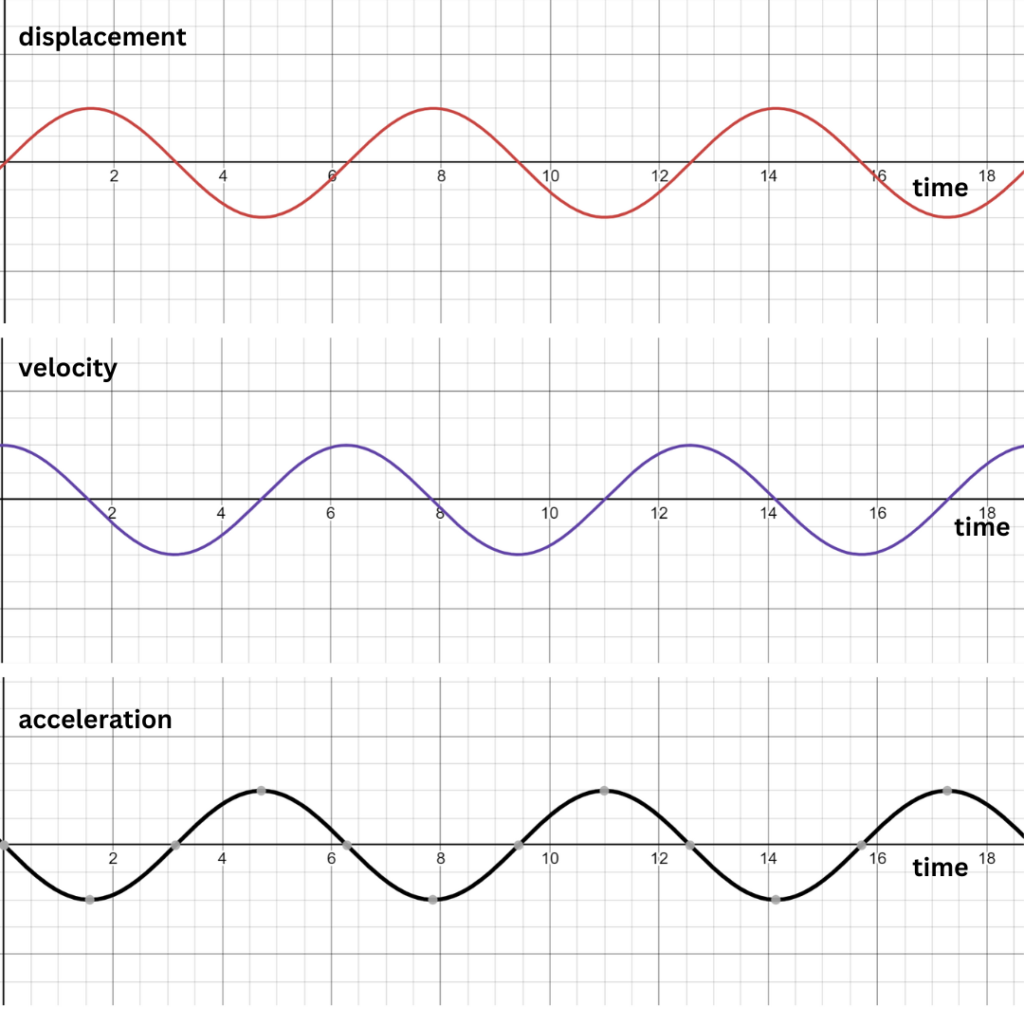
Here are some key terms when analyzing the graphs above:
- Amplitude (m) – The maximum displacement OR the highest point in the sinusoidal graph like the ones above.
- Period (s) – The time it takes to complete one oscillation. (To know this, you need to understand the trigonometric graphs)
- Frequency (Hz) – The number of oscillations in a period of time.
Comparing the graphs above, we can imply a few things:
- When displacement = 0, VELOCITY is MAXIMUM and ACCELERATION is ZERO.
- When velocity = 0, DISPLACEMENT is MAXIMUM and ACCELERATION is MINIMUM.
- Displacement –> velocity –> acceleration is a differentiation process.
2. Simple Harmonic Motion
Now that we get a grasp on common oscillations, we can start moving into a special type of oscillation known as Simple Harmonic Motion(SHM). SHM only happens when ALL the conditions below are met:
- There is a fixed cyclical path.
- There is a central equilibrium point.
- The motion repeats at equal time periods. (periodic)
- Displacement from equilibrium, velocity, and acceleration change continuously.
- There is a restoring force directed toward the equilibrium point.
It is important that you remember these points since theory-based questions are common in Paper 1 especially. But in case you don’t fully understand it right now, it’s fine, we will go through what each of them means as we progress through the topic!
First of all, I hope you guys remember what Force(N) is. It is a vector quantity that measures the amount of ‘push or pull’ or ‘action’ on an object. Net Force, is the TOTAL amount of force acting on the object. So if a force of 4N is acting to the right of an object, and a force of 2N is acting to the left, then the Net Force would be 2N to the right. (Always remember that in Forces, there should be negatives and positives depending on the direction of the force)
This is important since in SHM, the Net Force is always pointing towards the equilibrium. In terms of SHM, this Net Force is also known as Restoring Force. Looking at the pendulum example above, the net force of the bob will get directed towards the equilibrium(the position where Net Force is 0N). This means that if the pendulum swings to the right, the net force is directed at the left, causing the bob to slow down and eventually reach maximum displacement.
Once that happens, it starts moving towards the equilibrium position, to the left. This cycle then repeats until the pendulum stops, making it periodic and following a fixed cyclical path. As for point #4, it is clear from the graphs that the displacement, velocity, and acceleration of the pendulum bob is always changing since at NO point does it ever become a straight horizontal line.
Since F = ma, where m is mass measured in kilograms(kg), and a is acceleration measured in meters per second(m s-2), a new equation can be formed with the theory of Restoring Force:
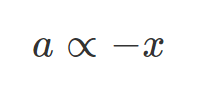
It simply means that acceleration is directly proportional to the opposite displacement. Keep in mind that the (-) symbol just indicates the direction of displacement. Quantity/value wise, when displacement increases, acceleration also increases. Likewise, this means that force is also directly proportional to displacement during SHM. Graphing this relationship would look something like this(x-axis is displacement; y-axis is force):
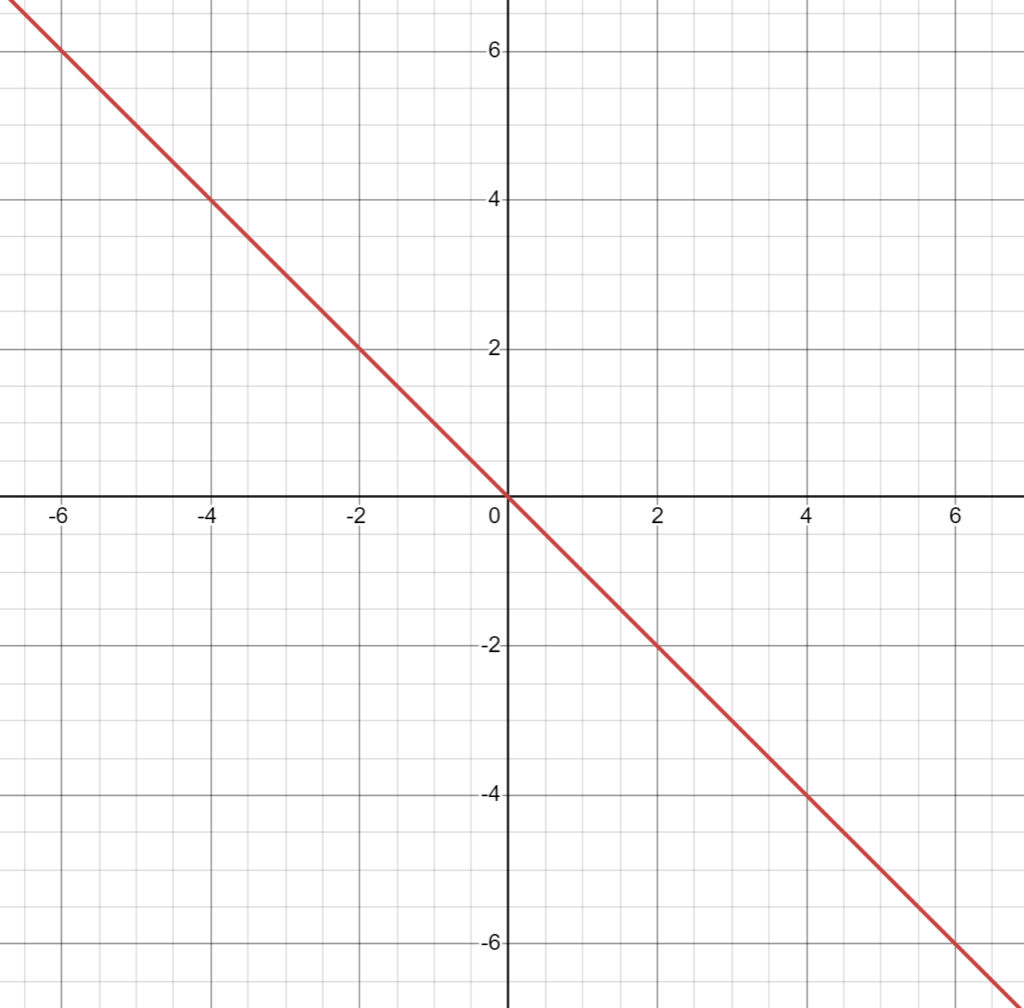
Important things to note:
- The line passes through the origin(0) which indicates that is is ‘directly proportional’.
- The line is linear, which means it is a straight line.
When the line is converted to standard equation form, it can be written as:
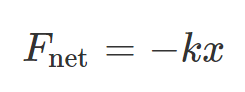
In this equation, ‘-k‘ is a constant and gradient of the line. Psst.. This will be important for HL students later on but for now just see it as a constant 😉
With this relationship, we get a clearer definition of Simple Harmonic Motion:
“SHM is defined as a motion arising from the acceleration of an object that is proportional to its displacement from a fixed equilibrium point and directed towards that point.”
OR
“SHM is defined as motion arising from a linear restoring force directed at a fixed equilibrium point.“
~Kognity
Now, with any system in Physics, laws of conservation need to be considered. Just in case you forgot, these are the rules that govern what can and cannot happen in nature. For SHM, the most important conservation law is for ENERGY. Because there is force and displacement in SHM, energy will be transfered, mainly Kinetic Energy(KE) and Gravitational Potential Energy(GPE) for pendulums and Elastic Potential Energy(EPE) for spring systems.
Continuing the pendulum example, imagine that when the pendulum is hanging straight down, the GPE of the system is 0. When the pendulum bob moves upwards, GPE increases since,
GPE = Mass x Gravitational Field x HEIGHT.
At the same time, KE will also be changing since velocity increases as the pendulum bob moves. However, as previously stated, when it hits the maximum displacement, the velocity is 0, thus KE is also 0. If we try to graph both KE and GPE in one plane, it would look like this(x-axis is displacement; y-axis is energy):
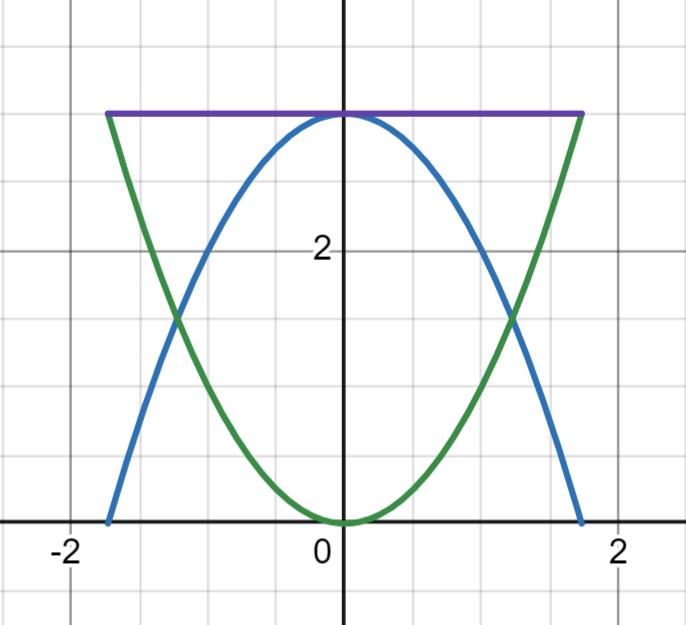
(Purple = TOTAL ENERGY, Blue = KINETIC ENERGY, Green = GRAVITATIONAL POTENTIAL ENERGY)
From the graph provided, can you guess which points are maximum displacement, and which is the equilibrium, on the x-axis?
Answer: The two x-intercepts of KE are the maximum displacement from the equilibrium while the intercept of GPE is the equilibrium.
Notice how the Total Energy remains fixed throughout the entire oscillation; this means that energy is conserved!!
3. Phase Shifts
You will probably see this term a lot in your Physics papers, and for a good reason. It refers to the difference in time of 2 sinusoidal waves. Normally, you will see it being represented in fractions or angles. So.. how does that look like? Here’s an example:
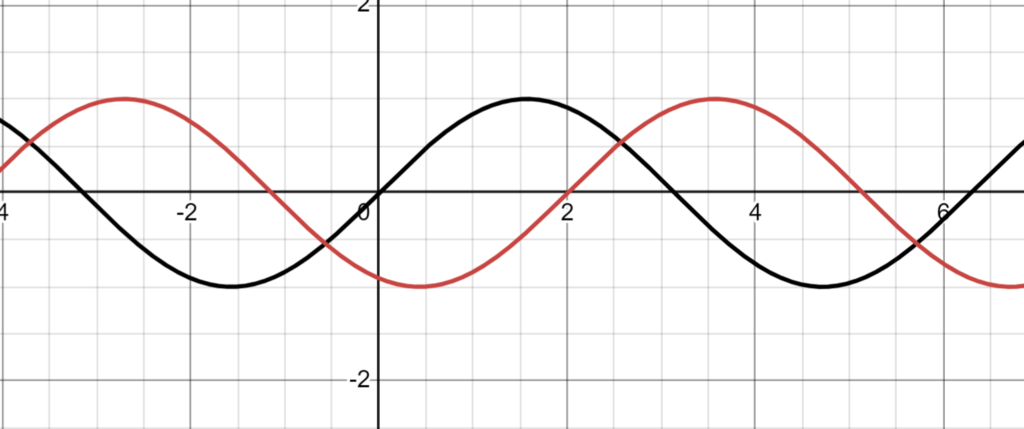
Analyzing the graph with the terms we learnt in section 1, amplitude appears to be the same. Since the curves are similar in horizontal length, period should also be the same. If you really look at it, it just appears that the red sinusoidal curve is SHIFTED to the right of the black curve. This here is called a ‘Phase Shift’. The most common angles for phase shift is: 0, π/2, π, 3π/2.
- 0 means that they are directly on top of each other.
- π/2 means that the top curves still intersect with one another, directly in the middle.
- π means that the positive and negative amplitudes are directly on top of each other(just like the displace and acceleration time graphs)
- 3π/2 is similar to π/2 but instead, the bottom is the one intersecting.
In case you want to confirm your answer or are given specific values, there is a formula that you can use to calculate this phase shift. The important factor you have to pay attention to is the X-AXIS and whether it is distance or time(The methods are actually the same but the variables are different). Here is the amazing formula:
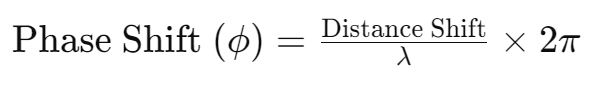
OR
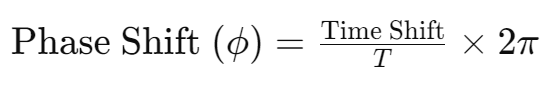
*Remember this formula since it won’t appear on your formula booklet.
4. Questions
Phew.. Okay, enough with the theory. Let’s apply what we learnt to some questions. Try to answer the questions without looking at the answers first!!
Question 1
Which of the following oscillations cannot be described as Simple Harmonic Motion(SHM)?
- A pendulum swinging back and forth.
- A car suspension system.
- A basketball bouncing on the floor.
- The air molecules oscillating near a vibrating guitar string.
Answer: #3. Do you remember the terms for SHM? The restoring force should be directly proportional to displacement from the equilibrium position. When gravity is acting on the basketball for #3, acceleration will be constant until it hits the ground, which means that it can’t be SHM since acceleration should change based on displacement as previously mentioned.
Question 2
Which of the following statements is true for a particle undergoing SHM?
- The particle’s speed is directly proportional to its displacement from the equilibrium position.
- The particle’s acceleration is always opposite sign to its velocity.
- The restoring force acting on the particle is directly proportional to its displacement from the equilibrium position.
- When the displacement of the particle from its equilibrium position is positive, the acceleration of the particle is positive.
Answer: #3. For this question, MAKE SURE YOU READ THE OPTIONS CAREFULLY. This question tries to trick you by changing ‘acceleration’ to ‘speed’ for option #1. Same as the reasoning from Question 1, restoring force is always directly proportional to its displacement from the equilibrium position.
Question 3
A child pushes down on a piece of wood floating on water, then releases the wood. The wood begins to oscillate with simple harmonic motion. The amplitude of the oscillation is 5cm and the maximum acceleration of the wood is 2 ms-2. What is the acceleration of the wood when it reaches its equilibrium position?
Answer: 0 ms-2. Aha, I found a calculation question! I would like to share my steps when to solve these types of question:
- Identify the independent, dependent, and control variables. In this question, the dependent variable is acceleration; this is the variable that is ‘affected’ by the independent variables. The independent variable is amplitude, since it talks about equilibrium position. In this case, there are no explicitly stated control variables or variables that do not change.
- Figure out what formulas to use in order to solve the problem. Since we are given amplitude(displacement) and acceleration, we can assume that we will need the relationship equation: a ∝ -x.
- Next, identify the values and their units. Notice how the amplitude is given in centimeters while acceleration is measured in meters. This would mean that some unit converstions would need to be done so that the values can be calculated and compared in the formula.
- Finally, solve the problem whether its a ratio or decimal!!
In this case, it’s kind of tricky since you don’t need to do steps 3 and 4. The question asks what happens to acceleration when it reaches equilibrium position, which basically means displacement = 0. This means that acceleration will also be 0 since it is directly proportional to displacement.
Question 4
Pendulum X oscillates in SHM with amplitude 3.0 cm. A second, identical pendulum Y is displaced by +5.0 cm and released into SHM precisely when X passes through its equilibrium position. What is the phase difference between X and Y?
Answer: π/2. Heres a trickier question for all of you. I’ll admit, I had a tough time understanding it myself at the beginning but let’s try it together. We are not given any information for wavelength and time, and when it comes to phase difference, amplitude does not really help either, so we can’t use the formula. What I do is I sketch it on a spare piece of paper(its not going to be drawn to scale).
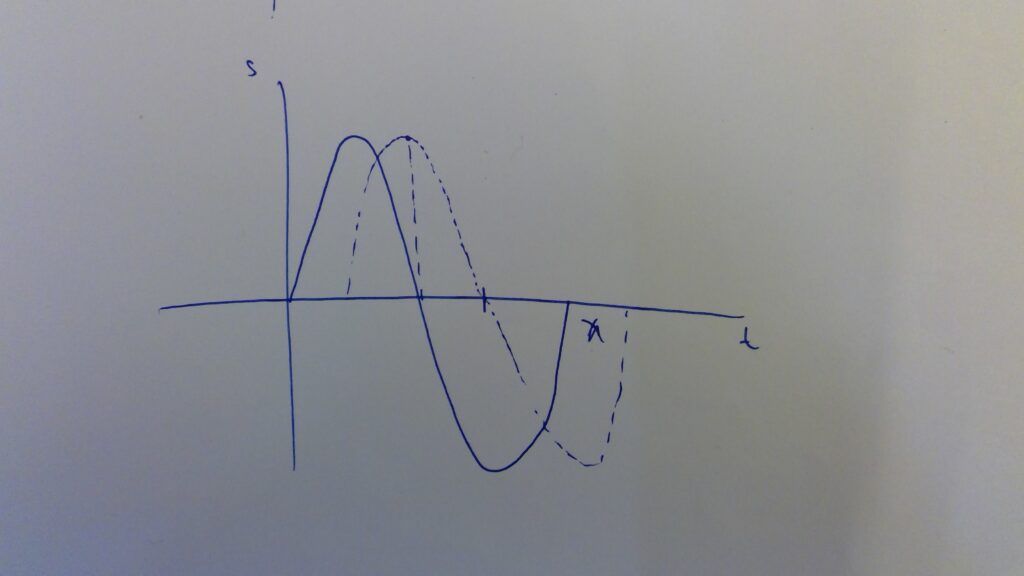
Looking at my amazing drawing, the solid curve is Pendulum X which is a typical sinusoidal curve. I didn’t plot any values since they were not going to help solve this problem. The hint we are given in the question is that Pendulum Y starts when X passes through equilibrium which means that displacement = 0. It then states that Pendulum Y is displaced by +5.0cm. This means that the bob is brought up to the maximum displacement, then released. Since they are identical pendulums, they have the same period. See where I drew the vertical dotted line, that’s where the oscillation for Pendulum Y starts. Knowing that, we can complete the oscillation and see that the phase difference is half of π since after completing the curve, it shows that there is a 1/4 gap, equivalent to π/2.
Alright, that’s all for Part 1 of Waves. The next time we will actually learn what a wave is 😀
For now go check out other blogs on subjects like Computer Science if you’re following that computer engineering route.



