Table of Contents
- The first basic formulas are:
- EXAMPLE QUESTION 1 (easy)
- The next six formulas are related to trigonometric functions:
- EXAMPLE QUESTION 2 (easy)
- Logarithms and natural logarithm formulas:
- EXAMPLE QUESTION 3 (easy)
- EXAMPLE QUESTION 4 (medium)
Before this revision starts, what type of integration questions appear in the IGCSE?
- Find the area under a curved graph,
- Reverse differentiation.
- Solve equations!!(Usually a lot of marks for one integration question)
Sometimes it might look confusing, and it is. Once we get to the harder equations, it will get a bit more confusing, but this will be a guide that starts from simple to difficult and makes sure that you understand every part of IGCSE integration to even the most complex questions.
But before we start there are a few equations that you have to remember that will make your journey much easier. It will go from easy to hard so you don’t get overloaded with equations.
The first basic formulas are:
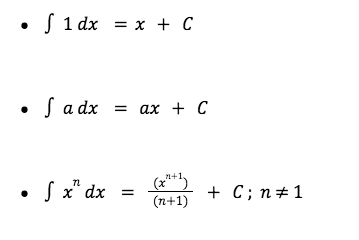
If you are new to integration, these few equations might look a bit difficult but it’s actually pretty simple.
For the first formula, if you see the number 1 integrated, it will immediately be x. We know this because if we differentiate x, we get 1. This proves that integration is basically reversing differentiation. Also make sure to add ‘+C’ at the end of your answer since every integration will have that “+C”.
The second formula means that if you see any number other than 1, your solution will be that value. Let’s say the question is ∫ 3 dx, your answer would simply be: 3x + C.
The third looks the most confusing but the formula is self explanatory. Let’s say you have the equation ∫ x^3 dx. The first step is to simply substitute the values to the formula. We will get:
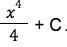
We can prove that this is right by deriving it. If we derive it, we will get x^3 which proves that the answer is correct.
There will be another way to determine if the answer is right using the calculator which will be demonstrated later.
EXAMPLE QUESTION 1 (easy)
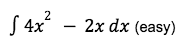
Hint: This question mostly uses the third formula. Try to do it yourself before I guide you through the question.
Answer:
So in order to find the answer, we have to split this equation into two parts. The first one is solving for 4×2 dx while the second one is 2x dx.
Because x has a power of 2, we will use the third formula. Just substitute the values to the formula:
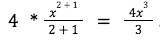
Now that we found the answer to the first part, the second part will be easy. Using basic logic, 2x dx will just be x^2. Yes this does not use any of the formulas mentioned above, but after learning differentiation, this problem should be simple. If we try to derive x^2, we will get 2x. So every time you have to integrate an x value with a coefficient, remember that the value is always x^n where n is the coefficient.
The final answer is:
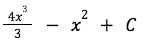
Alright!! If you understand how to do the question and formulas above, you are ready to move on to the next part. Don’t worry if you still don’t understand. Read through the formulas again and try to do some practice questions online similar to the one above.
The next six formulas are related to trigonometric functions:
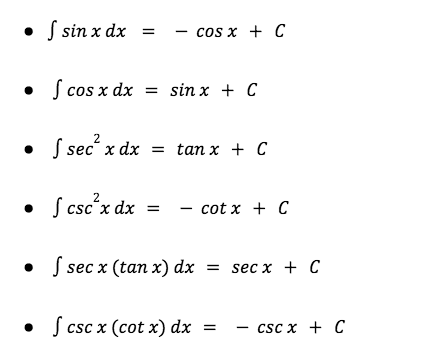
Now these formulas unlike the first ones are not as confusing. However, they may be often mixed up since there are so many of them. So.. you will unfortunately have to memorize these formulas down to the bone. But fear not! We will go through each of their uses using some examples later on to increase your memorization and understanding of these formulas.
** NOTE: This type of integration does not frequently appear on tests. Maybe 2 or 3 questions that specifically use trigonometric identities in integration.
EXAMPLE QUESTION 2 (easy)
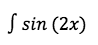
Now this is a very simple problem to solve, but it tells us more about trigonometric problems.
Since sine is used in this question, we can immediately know that we are supposed to use -cos x + C. But is that it? NO.
We have to remember that inside the sine brackets is 2x not just x. So we have to use a specific formula for that as well. If the value is any trigonometric function such as sin(nx) or cos(nx), we can remember that the integrated value will be multiplied by 1/n.
So in this case that value above will be 1/2.
The final answer is:
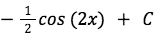
After understanding the trigonometric function integration, we are ready to move on to the last set of formulas.
Logarithms and natural logarithm formulas:
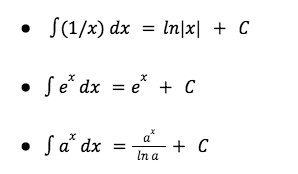
These formulas are fairly simple to remember.
For the first natural logarithm formula, just remember that if the question is 1 over an integer, x, the integrated value will be ln(x) + C.
For the second formula using e, every time there is e to the power of an integer, the integrated value will be the same and don’t forget to add “+C”.
EXAMPLE QUESTION 3 (easy)
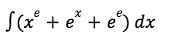
Like the question before, try your best to do the question first. If you’re done, check the answer below.
Like in Question 1, we can split up the equation into multiple integrations so we can focus on each one of them individually.
Splitting it will give us:
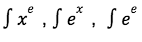
Now we can solve each one of them individually using the formula we learnt previously.
In order to solve the first part, we have to use the formula that we learnt in the very beginning. Although there is an e, we can treat it like an integer so that we can use the formula similar to the first question.
This will give us:
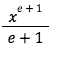
For the second part, exis just going to be the same according to the log formula.
Last but not least, eecan be treated like an integer so the integrated value would be eex using the logic method described in question 1.
The final answer is:
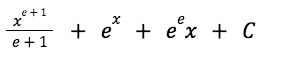
EXAMPLE QUESTION 4 (medium)
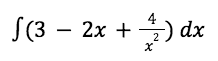
Alright, we are starting to get into intermediate territory. For this question, it follows the same steps. We have to first split it up. In a question like this, it is very easy to split up since the addition and subtraction are very clear.
Splitting it up will give us:
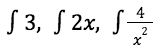
Another tip is that, it is better to ignore the symbols such as addition and subtraction in this type of question so that it’s easier to understand and solve.
Using the first formula, we can determine that the solution of the first part is just: 3x.
We can use differentiation logic to solve the second part which gives us: x^2.
Last but not least, the most complex problem here, we can solve this by first simplifying the equation:

Now we can use the third formula to integrate the smaller parts of the equation. This gives us:
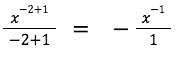
Now combine the 4 and the new equation above, we get:
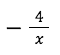
If we piece back the equations that we split with the addition and subtract symbols we get:
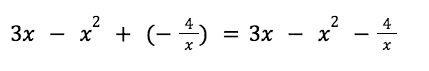
The final answer is:
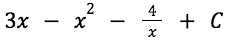
WOW!! Good job for making it this far. I knew you could do it! In order for you guys to not get overloaded, I will create a second blog related to the application of integration in graphs and numerical integration. Hopefully I managed to refresh your memory on integration or even teach you something new! Stay tuned for integration PART 2! 😀
P.s if you want to try out some integration questions on your own time, go check out this link. They have some challenging questions and answers to those questions.



