A concise and in-depth guide to learning differential equations, the final chapter within calculus! (You must have great prior knowledge on differentiation and integration before looking into differential equations as this this topic deals with both of those topics simultaneously.
Essential prior knowledge:
- Differentiation
- basic derivatives, product rule, chain rule
- Integration
- power rule, integration by substitution, by parts, by partial fractions
- Other topics mainly from topic 1, 2, 3
Click here to learn the rules of differentiation!
(Blog on integration rules coming soon…)
Table of Contents
Here are some differentiation and integration formulas you could refer to before I move on:

Differential Equations??????????
Is an equation that involves both the derivative of a function as well as the original function
Solutions of a differential equation
-Refers to the function y in terms of x that satisfies the equation
- Simple example: A solution to the equation dy/dx = y is y= e^x
- This is because when you differentiate y, it stays the same
- Another example: A solution to the equation dy/dx = 2xy is y = e^(x^2)
- If you differentiate e^(x^2), the answer would be 2xe^(x^2). To which is also equal to 2xy
General solution
In addition to the solution of y = e^x in the ‘simple example’ given above, there are several other solutions such as y = 2e^x, y = -9e^x, y = 4000e^x, and many more. All of these solutions are in the form of ce^x (you’re probably already familiar with the term ‘c’ which means constant from learning integration). This ‘ce^x’ is what we call the general solution to the differential equation dy/dx = y. This ‘general solution’ is essentially what we need to find within this topic, as answers to the hellish exam questions :’)
Now obviously the exam questions won’t be as easy as the aforementioned examples. (life is pain :’) ) Therefore… there are four main rules/formulas/techniques you could use to solve more complex differential equations:
- Variables separable
- Homogeneous form
- Integrating factor
- Euler’s method
Variables Separable!!!
Use this rule if you see that x and y are in two different functions! Or when you can separate the functions of x and y using algebra
Example of these types of questions:
- dy/dx = 3xlny
- (As you can see x and y are within two different/separate functions)
- dy/dx = xy – x
- In here you can separate the variables into x(y-1) through factorization, hence this rule is applicable for these types of equations as well!
- dy/dx = (y^2)/(1+x)
- This could be separated into dy/(y^2) = dx/(1+x)
Formula
This is easiest and quickest rule within differential equations so if it is applicable to solve the question, I highly recommend going for this rule right away!
Sample questions
SQ 1)

This was a relatively easy question. Now let’s do something more complex :3
SQ 2)


Woohoo! we got the final answer (That was easy wasn’t it? 😀 (I’m joking please don’t come @ me))
As you can see, we’ve used techniques and rules from many other topics such as logarithms and rules of integration, so it’s better to learn all the other topics first before this. I’d like to call this topic the final boss of math AAHL :’)
Homogeneous Form!!!
Some differential equations cannot be solved directly by separating the variables. Hence, the next step is to identify if the equation is in a homogeneous form. Which is when the the variable y is over x in the form y/x.
Example:
- dy/dx = (x + 2y)/x
- The x and y cannot be separated from one another
- This is equal to 1 + 2y/x
Formula

Sample questions
SQ 1)
^since y = vx, we multiply the whole equation by x, hence the general solution!
There might be questions where the values of x and y are given. In which we need to find not only the general solution, but the exact solution as well:
SQ 2)


There’s the exact solution and final answer!
As you can see with the given x and y values, we need to find the value of c which turns the general solution into an exact solution 🙂
Integrating Factor!!!
If none of the two previous techniques are applicable, this is the optimal solution!
Formula
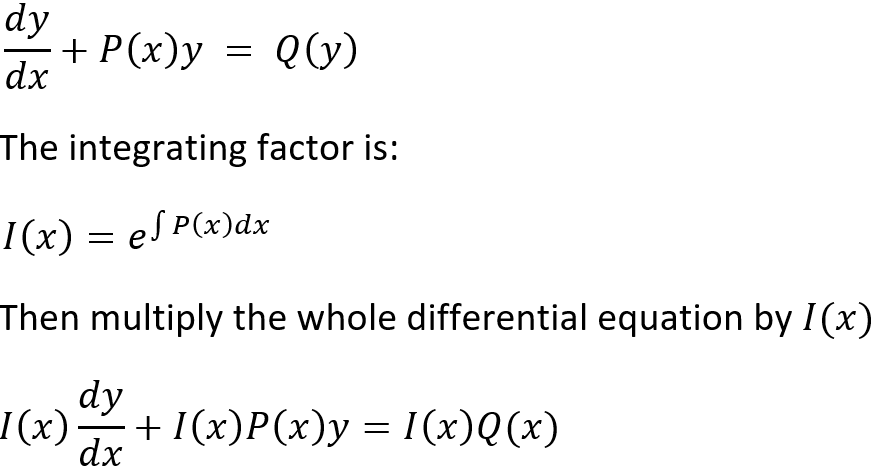
(You may be thinking “*Gasp* an integral as an exponent???” But fret not, it only looks complicated, and to be honest I’ve also thought that at first, but it is waaaay simpler than I could ever expect!)
Sample questions
SQ 1)

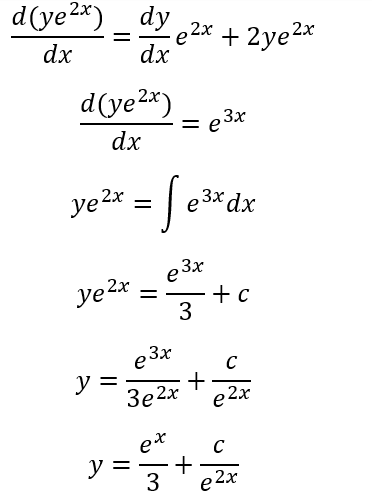
SQ 2)
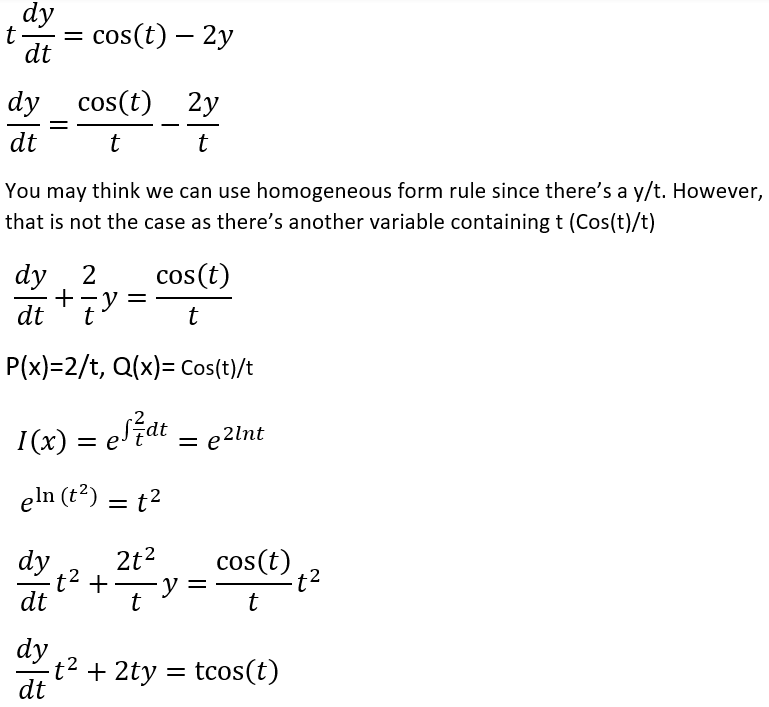

Euler’s Method for Numerical Integration!!!
This method doesn’t deal with a specific type of differential equation nor will we have to find the general solutions. Instead, we will find an approximate y value with a given x value
Formula
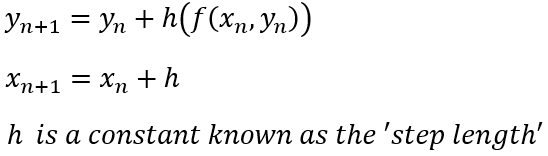
This may look intimidating, but don’t you worry it’s quite simple!
Let’s start with the examples now!
Sample questions
Typically, you use your GDC to do Euler’s method, but before that let’s start solving an example without the GDC to understand how this method works
SQ 1)
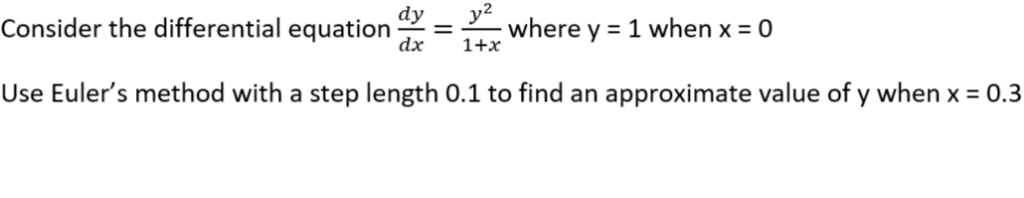
| n | x | y | f(x,y) = (y^2)/(1+x) |
| 0 | 0 | 1 | 1/(0+1) = 1 |
| 1 | 0.1 | 1+0.1(1)=1.1 | (1.1^2)/(1+0.1)=1.1 |
| 2 | 0.2 | 1.1+0.1(1.1)=1.21 | (1.21^2)/(1+0.2)=1.22008 |
| 3 | 0.3 | 1.21+0.1(1.22008)=1.33201 |
Now let’s do a question using the life-changing (yet boring) GDC
SQ 2)
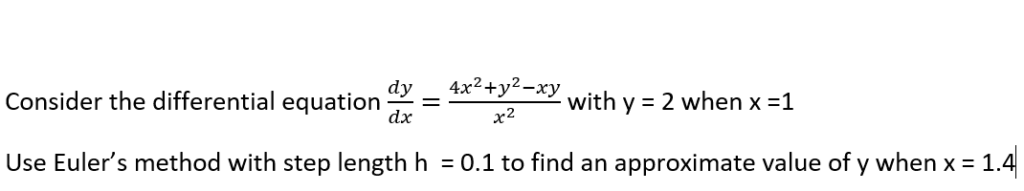
Let’s solve this question with the TI-84 GDC

There you go! I’d say there’s not much critical thinking needed for this method as you just need to memorize a few buttons is all
Yayy!! We’re done!!! Let us both get a 7 in IB Math AAHL 😉
Taking computer science as well? Here’s a summarized blog on system fundamentals!
Bibligraphy:
- https://id.pinterest.com/pin/2322237296316635/
- https://id.pinterest.com/pin/17944098507577987/
- https://id.pinterest.com/pin/249668373087324621/
- https://id.pinterest.com/pin/2955555999598785/
- https://id.pinterest.com/pin/832673418607794436/
- http:/MathsTutorGeneva.ch/



