IB Mathematics HL Analysis and Approaches Calculus 101: Rules of differentiation simplified ;3 (Product rule & Chain rule)

Follow me to unravel the complexities of differentiation! The most essential and basic part of calculus. I truly am positive, this blog will boost your confidence on the dreadful topic, Calculus!

Common derivatives

Before we proceed towards the rules/techniques of differentiation, here are a couple of derivatives to keep in mind if you don’t already know yet 🙂

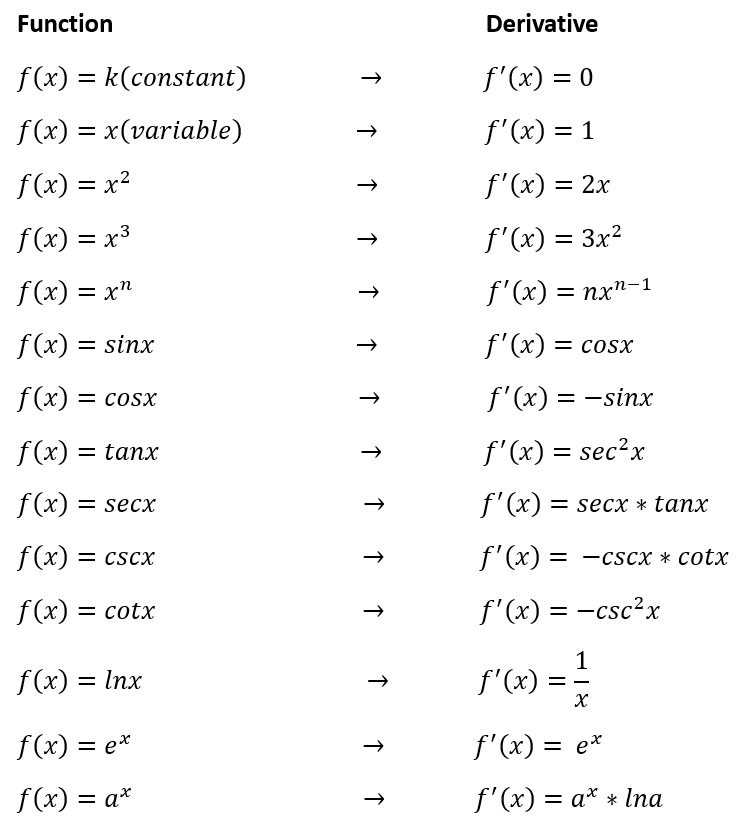
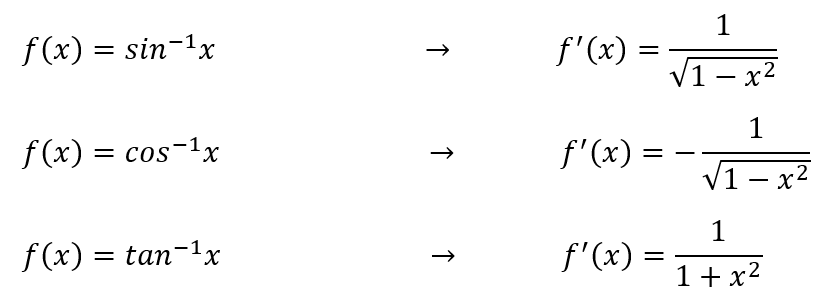
The functions above can be differentiated immediately, but what if the given function in the question cannot be differentiated immediately? Now that’s what the product rule and chain rule are for

The Product Rule for Differentiation!!!

The product rule is used in differentiation when two (or more) functions/variables are multiplied to one another, in the form of f(x)*g(x)

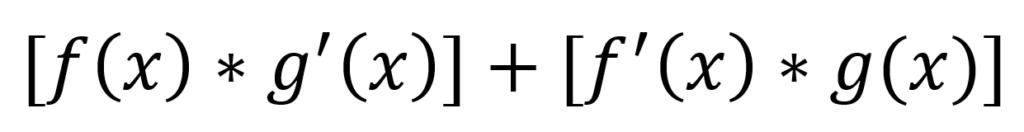
Here’s a simple example to apply these steps!

Example 1: Differentiate xsinx

Solution:

As we can see, there are two functions/variables multiplied to one another, ‘x’ and ‘sinx’.

let f(x) = x and g(x) = sinx

(1) f(x) * g'(x) = x * cosx = xcosx

(2) f'(x) * g(x) = 1 * sinx = sinx

(3) (1) + (2) = sinx + xcosx

Hence the final answer is sinx +xcosx

Example 2:

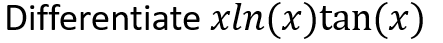
Solution:

In this case there are three variables so what do we do????? OH NO it’s the end of the world!!!

Nah I’m kidding, fret not as it is much simpler than you think 😉

let u = x

v = ln(x)

w = tan(x)

Step 1: Differentiate u and multiply with the normal v and w

Step 2: Differentiate v and multiply with the normal u and w

Step 3: Differentiate w and multiply with the normal u and v

Step 4: Add all the steps together

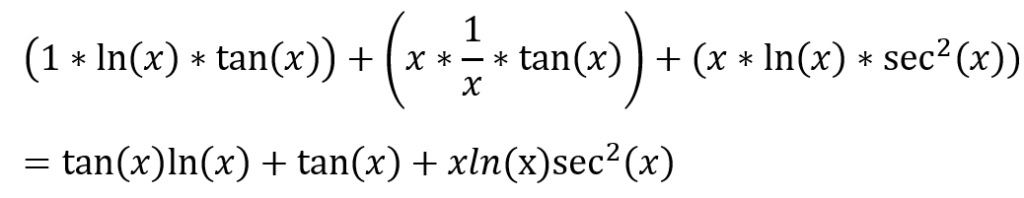
See! Not too bad right? 😀 (Smiling through the pain)

Now here are some questions on product rule that you can solve by yourself 🙂 (answers at the end of this blog, but please try your best before looking at the answers)

Section A) Differentiate the following:

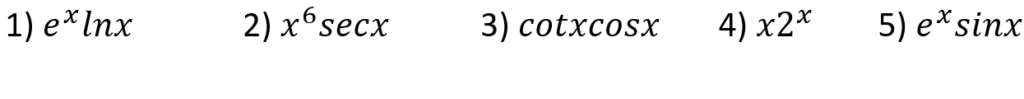
The Chain Rule for Differentiation!!!

^Imagine an onion, considering the fact that it has 2 or more layers. You will have to firstly peel out the outer layer in order to peel out the inner layer, and it keeps going on and on until you can’t peel anymore. That’s basically what the chain rule is!

The chain rule is used in differentiation when one or more functions is inside another, which is in the form of f(g(x)) or f(g(h(x))) and so on

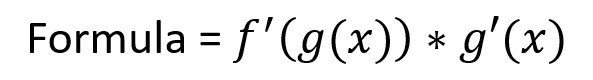
Let’s say you have two functions, with one function being inside another. Let’s name the inner function g(x) and the outer function f(x)

(1) differentiate the outer-most function which is f(x), and keep the inner function the same

(2) Completely ignore the outer function, and just differentiate g(x)

(3) Multiply the results from step 1 and 2 together and voila! You get your answer

Chain rule is more complicated that product rule so it may be more confusing when explaining it verbally so let’s start with the examples

Example 1:

It is also possible that there are three or more functions within one another. So here’s an example with 3 functions

Example 2:

Now here are some questions on chain rule that you can solve by yourself 🙂 (answers at the end of this blog, but please try your best before looking at the answers)

Section B) Differentiate the following:

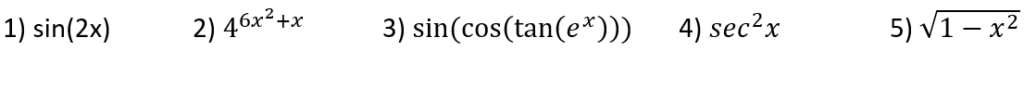
Combination of both rules, and more…

As you have probably noticed, I did not include the quotient rule. This is because I believe that quotient rule is not necessary as it is takes too much time. Here! Let me show you a trick on how you can use both chain rule and product rule in a way that you do not need to use quotient rule anymore. Here’s an example:

I believe this to be a way more efficient method than memorizing the quotient rule as quotient role tends to get veeeery lengthy so I hope you will find this tip helpful

Moving on, there may be some cases where the variable and its exponent are both variables with neither of them being constants, so how do you solve them?:

Reflecting upon the two examples given above, you may have observed that in some cases, you don’t need or can’t apply product rule and chain rule immediately since you may have to simplify the given functions first, to the point you are able to apply any of the rules in order to come up with your final answer.

Here are some questions that require you to use both the aforementioned rules:

Section C) Differentiate the following:

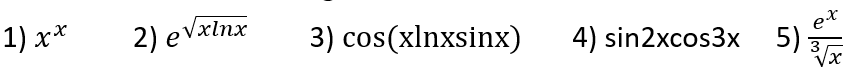
Answers

Section A:

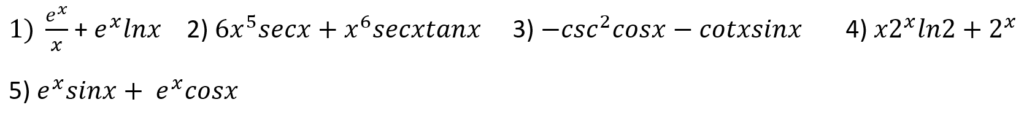
Section B:

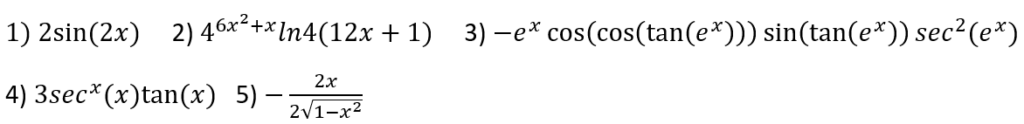
Section C:

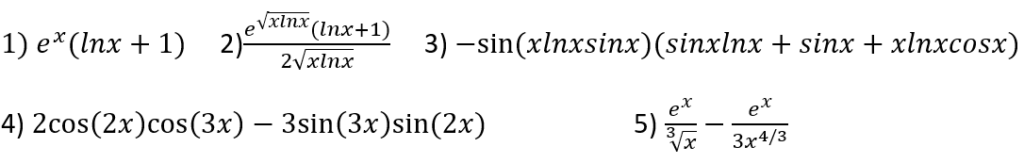
Thank you for taking a look into this blog! Hope you found the tips and information here helpful, let’s hope to get a 7 in Mathematics 😀

Want to learn the other half of calculus, integration? check out this blog right here 😉

Bibliography:

https://www.vecteezy.com/free-vector/onion