Mathematics AI: A Small Introduction to Hypothesis Testing
In mathematics applications and interpretation, there is a chapter focusing on hypothesis testing. But what is hypothesis testing? It is a topic in the statistics and probability category, in which this type of test uses a sample from a group of data in a an experiment to test out a statement made about the population.
Important Note: A statement in hypothesis testing is either about a population parameter or the distribution of the population.
Chapter 16: Hypothesis Testing
T-Test: A statistical method of comparing the means of two groups of data.
Null Hypothesis: it is the assumption that there is no change or difference between two groups, or no relationship between two variables.
- A null hypothesis is assumed to be true unless there is enough evidence to reject the claim.
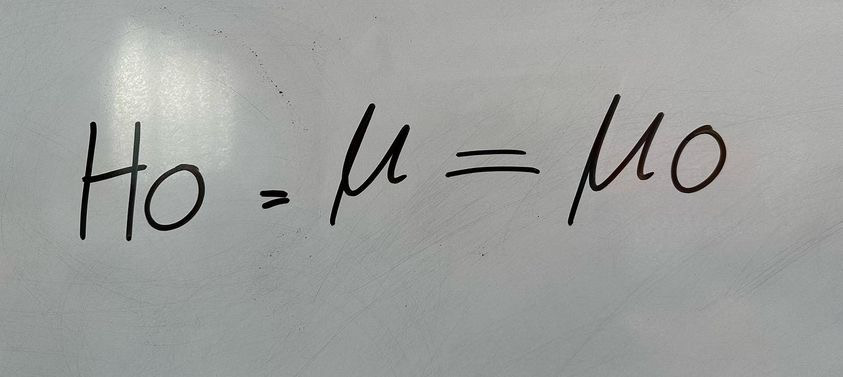
Alternative Hypothesis: it is the statement shown if there is a change or difference between two groups, or a relationship between two variables.
- If the P-Value is lesser than the Level of Significance, we reject the null hypothesis.
- If the P-Value is greater than the Level of Significance, we do not reject the null hypothesis.
If the null hypothesis is equal, the alternative hypothesis could be:
H1: The Mu (also known as the mean) of one population > is greater than the mean of another population.
H1: The Mu of one population < is lesser than the mean of another population.
H1: The Mu of one population ≠ is not equal to the mean of another population.

Important Note: The null hypothesis H0 always states that M is equal to a specific value.
To find T-Test using the Ti-48 calculator: Stat -> 1 : Edit -> Enter the values -> Select TESTS – :4 : 2-SampTTest -> Inpt: Data -> Choose parameter (your alternative hypothesis) -> Pooled: Yes -> Select Calculate -> Enter
Two Sample Questions!
Q1. Two IB schools would like to compare the test results of their students. They randomly pick 10% of their second year students and check their test results on a test where the maximum marks was 60. The table below shows the results.
| School A | 48 | 40 | 53 | 48 | 45 | 57 | 54 | 46 | 47 |
| School B | 50 | 46 | 49 | 43 | 45 | 52 | 32 |
Assume that the test results follow a normal distribution and the variance is the same in the two schools.
A.) State the appropriate null and alternative hypothesis for the two sample t-test.
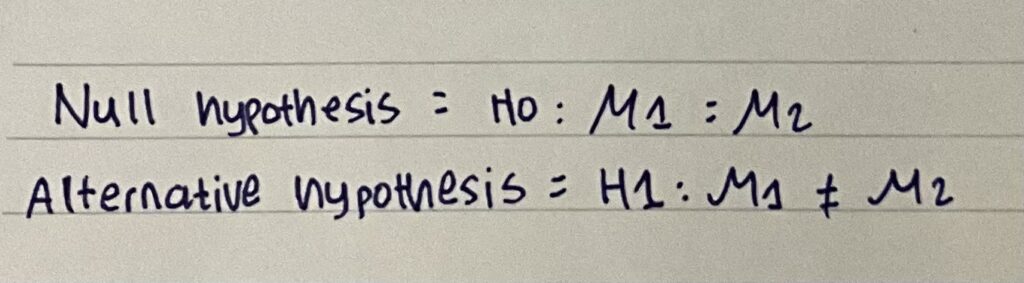
Now, why is the alternative hypothesis not equal to? If you look at the question, it doesn’t mention whether there is an increase or decrease in the values. So, this makes the alternative hypothesis not equal.
B.) Find the P-Value.
Now, remember the flowchart to find the T-Test (scroll above!) After entering the values into L1 and L2 into your calculator, select stat once again, select TESTS, and choose 4 : 2-SampTTest. After selecting the choices from the given data, and you select calculate, there would be the value of p given.
In this case, the P value for this question would be 0.2708304641, and then rounded off to 0.271
C.) Draw a conclusion at a 10% level of significance.
Our given P-Value is 0.271, and our level of significance is 10%. Convert it into decimal, and we get 0.1, so that means 0.271 > 0.1
And since our P-Value is greater than our significance level, we do not reject the null hypothesis.
Q2.) Determine if a new antibiotic cream will help heal a cut faster than the existing treatment will. The data for the two groups are given to perform a hypothesis test in order to determine if the new cream decreased the healing time of a cut with a 5% level of significance.
| New Cream | 3 | 5 | 4 | 6 | 6 | 5 | 3 | 2 | 3 | 4 | 5 | 3 | 4 |
| Old Cream | 4 | 6 | 6 | 7 | 6 | 4 | 4 | 4 | 3 | 6 | 5 | 4 | 5 |
A.) Determine the null and alternative hypothesis.
Notice how they mentioned “decreased” in the question? So this makes our alternative hypothesis the mean of one group of data being lesser than the mean of another group of data.
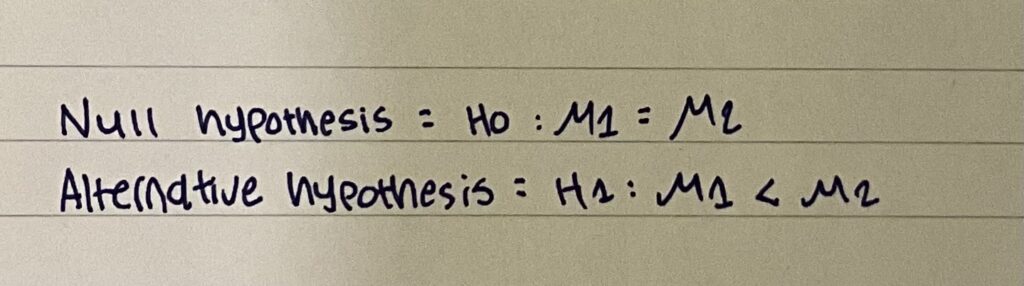
B.) Find the P-Value
For this question, following the similar steps above in the previous question, our P-Value would be 0.0451276864, and then rounded off to 0.0451
C.) Draw a conclusion at a 5% level of significance.
Our given P-Value is 0.0451, and our level of significance is 5%. Convert it into decimal, and we get 0.05, so that means 0.0451 < 0.05
And since our P-Value is lesser than the level of significance, we reject the null hypothesis.

That’s all for today folks! If you wish to check out other blogs surrounding the IB programme, you can check them out here!
Thank you for reading! Jia You!
Links used in this blog: https://www.pexels.com/photo/opened-book-240163/



